Uniform integrability

The concept of uniform integrability is an important concept in functional analysis and probability theory.

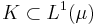If $\mu$ is a finite measure, a subset $K \subset L^1(\mu)$ is said to be uniformly integrable if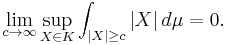 $\lim_{c \to \infty} \sup_{X \in K} \int_{|X|\geq c} |X|\, d\mu = 0.$

Rephrased with a probabilistic language, the definition becomes : a family 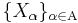$\{X_{\alpha}\}_{\alpha\in\Alpha}$ of integrable random variables is uniformly integrable if

$\sup_{\alpha}\mathrm{E}\left[ |X_{\alpha}| I_{\{|X_{\alpha}| > c\}} \right]\to 0,\; c\to\infty.$

This definition is useful in limit theorems, such as the Vitali convergence theorem.

1 Sufficient conditions
2 Sufficient and necessary conditions
3 Relations to convergence of random variables
4 See also
5 Notes
6 References

Sufficient conditions

If 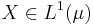$X \in L^1(\mu)$ , the singleton 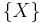$\{X\}$ is uniformly integrable, as an easy consequence of Lebesgue's dominated convergence theorem. Similarly, finite subsets of 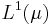$L^1(\mu)$ are uniformly integrable.

If 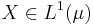$X \in L^1(\mu)$ , the set 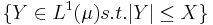$\{ Y \in L^1(\mu) s.t. |Y| \leq X \}$ is uniformly integrable.

A set bounded in 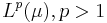$L^p(\mu), p>1$ is uniformly integrable.

Sufficient and necessary conditions

Bounded and absolutely continuous

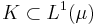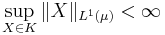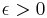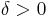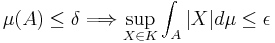A subset $K \subset L^1(\mu)$ is uniformly integrable iff it is uniformly bounded (i.e. $\sup_{X \in K } \| X\|_{L^1(\mu)} <\infty$ ) and absolutely continuous, i.e. for any $\epsilon >0$ there exists $\delta > 0$ so that $\mu(A) \leq \delta \Longrightarrow \sup_{X \in K} \int_A |X| d\mu \leq \epsilon$ .

Dunford–Pettis theorem

A subset 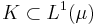$K \subset L^1(\mu)$ is uniformly integrable if and only if it is relatively compact for the weak topology.

de la Vallée-Poussin theorem^[1]

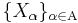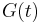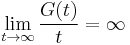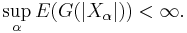
The family $\{X_{\alpha}\}_{\alpha\in\Alpha}$ is uniformly integrable iff there exists a nonnegative increasing convex function $G(t)$ such that $\lim_{t \to \infty} \frac{G(t)}{t} = \infty$ and $\sup_{\alpha} E(G(|X_{\alpha}|)) < \infty.$

Relations to convergence of random variables

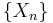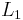A sequence $\{X_n\}$ converges to $X$ in the $L_1$ norm if and only if it converges in measure to $X$ and it is uniformly integrable.

In probabilistic language, a sequence of integrable random variables 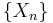$\{X_n\}$ converges to $X$ in mean if and only if it converges in probability to $X$ and it is uniformly integrable.

Notes

^ Theorem T22, P. A. Meyer (1966).

References

A.N. Shiryaev (1995). Probability, 2nd Edition, Springer-Verlag, New York, pp. 187–188, ISBN 978-0387945491

Walter Rudin (1987). Real and Complex Analysis, 3rd Edition, McGraw–Hill Book Co., Singapore, pp.133, ISBN 0-07-054234-1

J. Diestel and J. Uhl (1977). Vector measures, Mathematical Surveys 15, American Mathematical Society, Providence, RI ISBN 978-0821815151

Paul-André Meyer (1966). Probability and Potentials, Blaisdell Publishing Co, N. Y.